Study Guide

Field 182: Elementary Mathematics Specialist 
Sample Selected-Response Questions

Recommendation for individuals using a screenreader: please set your punctuation settings to "most."

Expand All | Collapse All

General Test Directions

This test consists of two sections: 1) a section with selected-response questions and 2) a constructed-response section.

Each question in the first section is a selected-response question with four answer choices. Read each question and answer choice carefully and choose the  start uppercase ONE end uppercase  best answer.

Try to answer all questions. Even if you are unsure of an answer, it is better to guess than not to answer a question at all. You will  start uppercase NOT end uppercase  be penalized for guessing.

The second section of this test consists of one constructed-response assignment. You will be asked to provide a written response to the assignment. Directions for completing your written response to the constructed-response assignment appear immediately before the assignment.

Reference materials will be available to you during this test. To access these reference materials, click on the reference materials icon located in the lower left corner of the screen.

You may  start uppercase NOT end uppercase  use any type of calculator or outside reference materials during this testing session.

Sample Selected-Response Questions

Competency 0001 
Apply knowledge of number sense, number systems, and the properties of the real number system.

1. A sixth-grade teacher introduces which of the following vocabulary terms to describe any number that can be written as a fraction?

  1. integers
  2. natural numbers
  3. rational numbers
  4. whole numbers

Correct Response: C. A rational number is the ratio of two integers where the denominator is not equal to zero. a over b, a and b are both integers and b does not equal 0.

Competency 0002 
Analyze number operations and computational algorithms.

2. A third-grade teacher is introducing their students to the inverse relationship between multiplication and division. Which of the following pairs of equations would best demonstrate this relationship?

  1. 3 multiplied by 4 equals 12 and 4 multiplied by 3 equals 12
  2. 12 divided by 3 equals 4 and 12 divided by 4 equals 3
  3. 3 multiplied by 4 equals 12 and 12 divided by 2 equals 6
  4. 12 divided by 3 equals 4 and 4 multiplied by 3 equals 12

Correct Response: D. An inverse relationship means that one operation can “undo” the other operation. Multiplication and division are the opposite of each other. The same numbers are used in both equations while one is a division equation, and one is multiplication.

Competency 0003 
Apply knowledge of patterns, algebraic and proportional reasoning, expressions, and equations.

3. A tortoise and a hare are 500 meters apart. The tortoise begins traveling away from the hare at a rate of 25 meters per minute. Ten minutes later, the hare starts running toward the tortoise at a rate of 225 meters per minute. Which of the following equations could be used to find x, the number of minutes that the tortoise travels before the hare catches up to it?

  1. 25 times the quantity of x minus 10 equals 225 x
  2. 25 x plus 225 x minus 10 equals 500
  3. 500 plus 25 x equals 225 times the quantity x minus 10
  4. 225 x minus 10 minus 25 x equals 500

Correct Response: C. Using the equation rate multiplied by time equals distance, at time = x minutes, the tortoise is 500 plus 25 x meters from the hare's starting position. The hare starts ten minutes later, so its time is x minus 10, and its distance from the starting position is 225 times the quantity x minus 10. In order to catch up to the tortoise, the hare's distance must equal the tortoise's distance, so 500 plus 25 x equals 225 times the quantity x minus 10. The left side of the equation is their distance apart, the rate of the tortoise using the given 25 meters, and the unknown. The right side of the equation is the rate of the hare times the unknown and ten subtracted from it. By setting the distance and rate of each animal opposite to each other, solving for x will determine the number of minutes the tortoise will travel before the hare catches up to it.

Competency 0004 
Apply knowledge and concepts of linear functions to model and solve problems.

4. A transformation applied to the linear function y equals 2 x minus 3 results in the linear function y equals 2 x plus 7. Which of the following statements describes the results of this transformation on the graph of y equals 2 x minus 3?

  1. The graph shifts up 7 units.
  2. The graph shifts up 10 units.
  3. The graph shifts left 7 units.
  4. The graph shifts left 10 units.

Correct Response: B. The equation of a line is y equals m x plus b , where b is the y-intercept. Since the quantity 2 x minus 3 plus 10 equals 2 x plus 7, each y-value of y equals 2 x plus 7 is 10 units higher than the corresponding y-value of y equals 2 x minus 3, so the graph of y equals 2 x minus 3 has shifted up 10 units.

Competency 0005 
Apply knowledge and concepts of Euclidean, transformational, and coordinate geometry.

5. Use the image below to answer the question that follows.

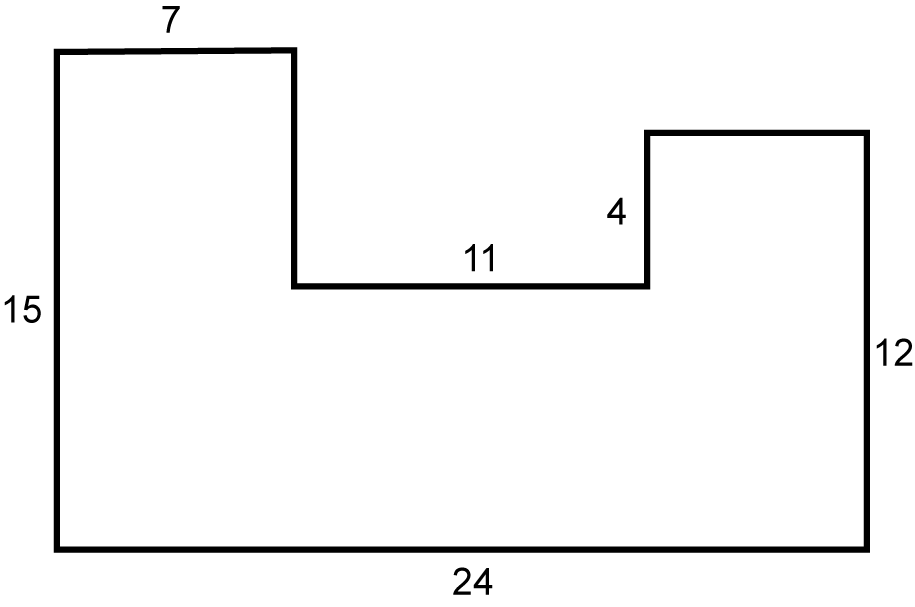
An irregular octagon with 8 right angles and an indented center on the top. The bottom length is labeled 24. The height of the left side is labeled 15 and the height of the right side is labeled 12. The top side is many different measurements. There is a length of 7 followed by an unlabeled height. Then there is a length of 11 followed by a height of 4. The final side of the top is an unlabeled length.

What is the area of this figure?

  1. 316 square units
  2. 265 square units
  3. 86 square units
  4. 73 square units

Correct Response: B. Since all the angles are right angles, we know each side is parallel and the total length will equal the length of the opposite side. The shape can be broken into three rectangles, and then add the total of the three areas to find the total area. 7 multiplied by 7 equals 49, 6 multiplied by 4 equals 24, 24 multiplied by 8 equals 192. 49 plus 24 plus 192 equals 265 square units.

Competency 0006 
Apply knowledge and concepts of measurement.

6. An observer at a baseball game sees a batter hit the ball and then hears the sound of the hit 0.4 seconds later. If sound travels at 1,225 kilometers per hour, which of the following expressions could be used to estimate the distance in meters between the batter and the observer?

  1. the quantity 1,225 times 0.4 divided by the quantity 1,000 times 60 times 60 meters
  2. the quantity 1,225 times 1,000 times 60 times 60 divided by the quantity 0.4 meters
  3. the quantity 1,225 times 60 times 60 divided by the quantity 1,000 times 0.4 meters
  4. the quantity 1,225 times 1,000 times 0.4 divided by the quantity 60 times 60 meters

correct response: D. Dimensional analysis is used to represent and solve problems. Use unit conversions and cancellation of units as follows:

The quantity 1,225 kilometers divided by 1 hour times the quantity 1,000 meters divided by 1 kilometer times the quantity 1 hour divided by 60 minutes times the quantity 1 minute divided by 60 seconds times the quantity 0.4 seconds divided by 1.

All units cancel except meters.

Competency 0007 
Analyze and interpret data.

7. Use the graph below to answer the question that follows.

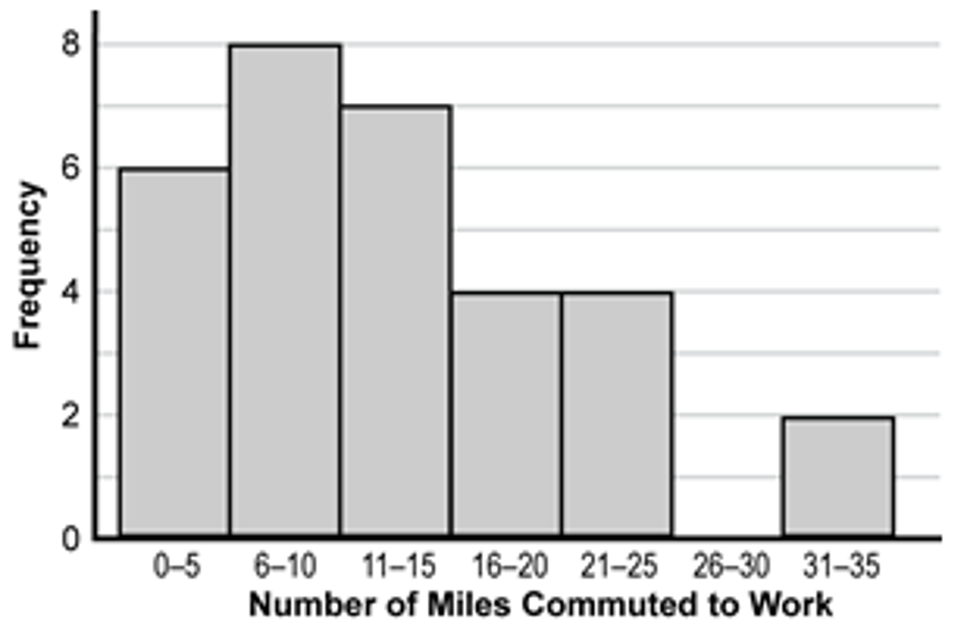
A bar graph with the horizontal axis labeled Number of Miles Commuted to Work and the vertical axis labeled Frequency. There are 6 bars for 7 spots on the x axis. The 0 to 5 bar goes up to the 6 on the Frequency axis. The 6 to 10 bar goes up to the 8 on the Frequency axis. The 11 to 15 bar goes up to the 7 on the Frequency axis. The 16 to 20 bar and the 21 to 25 bars both go up to the 4 on the Frequency axis. There is no bar for the 26 to 30 spot. The 31 to 35 bar goes up to the 2 on the Frequency axis.

Each of the workers at a company has reported the number of miles they commute to work each day. The data are compiled in the graph above. Which of the following box plots could represent the data?

  1. There is a number line labeled Miles Commuted with a box plot above it. The number line is labeled 1, 7, 12, 19, 32. The whiskers of the plot reach to 1 and 32. There is a box from 7 to 19 with a vertical line at 12.
  2. There is a number line labeled Miles Commuted with a box plot above it. The number line is labeled 2, 5, 13, 16, 33. The whiskers of the plot reach to 2 and 33. There is a box from 5 to 16 with a vertical line at 13.
  3. There is a number line labeled Miles Commuted with a box plot above it. The number line is labeled 1, 12, 15, 18, 33. The whiskers of the plot reach to 1 and 33. There is a box from 12 to 18 with a vertical line at 15.
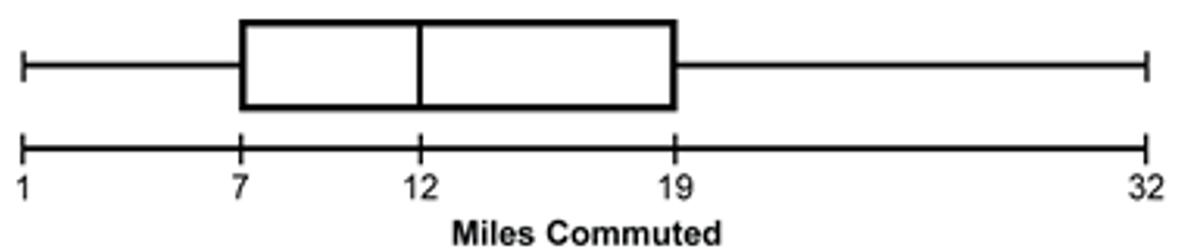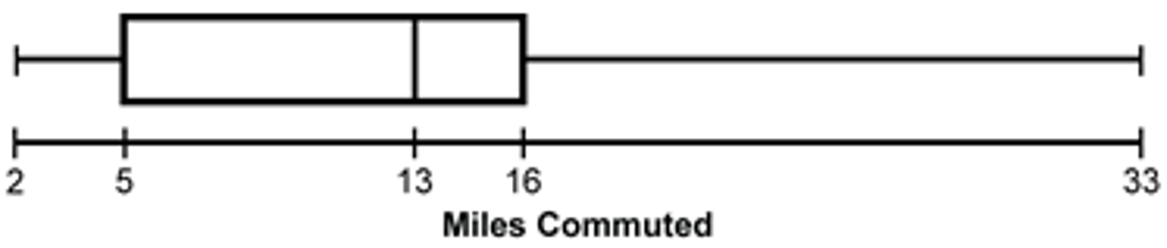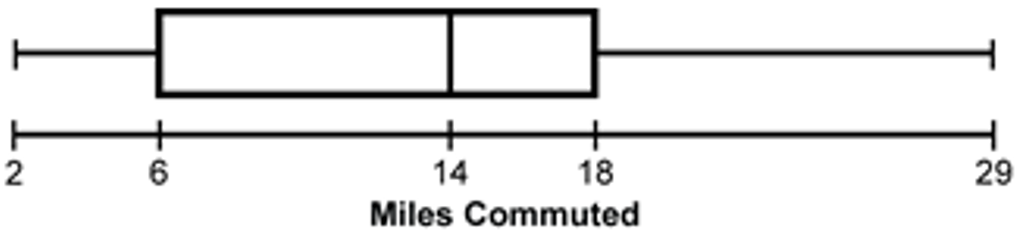  4. There is a number line labeled Miles Commuted with a box plot above it. The number line is labeled 2, 6, 14, 18, 29. The whiskers of the plot reach to 2 and 29. There is a box from 6 to 18 with a vertical line at 14.

Correct Response: A. According to the data in the graph, the range of the box plot needs to include a lowest number between 0 and 5 and a highest number between 31 and 35, so choice D is not possible. When the 31 data values from the graph are listed in increasing order, the median is the 16th value, which is between 11 and 15. The first quartile value is the 8th data value, which is between 6 and 10. Choice A is the only plot for which both of these statements are true.

Competency 0008 
Apply knowledge and concepts of probability.

8. A small store sells one-gallon containers of different kinds of milk. The store keeps track of the number of gallons sold for each kind of milk over the course of a month. The data are shown in the table below.


Milk Gallons sold by Type in a month
Type of Milk Gallons Sold in a Month
whole 22
low-fat 20
skim 18
chocolate 15

On Monday, the store sold 2 gallons of milk. If a stockperson immediately replaces each gallon as it is sold, what is the probability that at least one of the gallons sold was chocolate?

  1. 9 twenty-fifths
  2. 3 fifths
  3. 16 twenty-fifths
  4. 4 fifths

Correct Response: A. The probability that at least one of the gallons sold is chocolate equals one minus the probability that both gallons sold are not chocolate. probability of one not chocolate equals the quantity 22 plus 20 plus 18 over the quantity 22 plus 20 plus 18 plus 15 equals 4 fifths. Because the gallons are replaced as soon as they are sold, probability of both not chocolate equals 4 fifths times 4 fifths, so probability of at least one chocolate equals 1 minus 16 twenty-fifths equals 9 twenty-fifths.

Competency 0009 
Demonstrate knowledge of mathematics instruction and assessment.

9. At the beginning of the new school year, a second-grade teacher administers a pretest to determine how well students managed to retain basic arithmetic skills over the summer break. The teacher and the Elementary Mathematics Specialist are pleased to discover that many of the students were able to add and subtract numbers from 1 to 20 accurately and without using their fingers. In order to facilitate continued student growth in this area, which of the following instructional activities would it be most appropriate for the Elementary Mathematics Specialist to suggest first?

  1. guiding students to explore the computational algorithms they are employing
  2. having students use manipulatives to visually illustrate the problems they are solving
  3. asking students to explain the metacognitive processes they are using to solve the problems
  4. providing students with more complex problems that include numbers from 1 to 50

Correct Response: A. Since the pretest shows that many students are able to add and subtract numbers from 1 to 20 accurately, asking them to explore the algorithms they are using will improve their depth of understanding of why the algorithms work and allow students to extend these algorithms to operations with larger numbers.

Competency 0010 
Demonstrate knowledge of instructional leadership in mathematics.

10. An Elementary Mathematics Specialist is reviewing recent standardized assessment data that show that the overall performance of students in the school is below expectations in several key areas of mathematics. The Elementary Mathematics Specialist can best promote positive changes in the school's mathematics curriculum and instruction by taking which of the following steps first?

  1. developing a comprehensive written plan of action to address the data and presenting it to the Board of Education for approval
  2. communicating the data to teachers and engaging them in a dialogue to develop a clear shared purpose
  3. redesigning the school mathematics curriculum in light of the data and working with the teachers to implement it
  4. researching professional development options and recommending particular professional development opportunities for specific teachers

Correct Response: B. To best promote changes, it is necessary that the teachers recognize and support the purpose of the changes. Communicating the data to the teachers allows them to recognize needs and engaging them in a dialogue allows them to share in evaluating and improving instruction, thereby gaining their support.